[abstract]

• propose Search to Aggregate NEighborhood (SANE)
  • automatically design data-specific GNN structures
• propose differentiable search algorithms

[1. Introduction]

• problem of GNN
  • 모든 task에서 best performance를 내는 single model 없음
  • 같은 task, 다른 dataset에서의 optimal model이 없음

• 현재: neighbors의 hiden feature를 aggregate하기 위해 같은 aggregation function으로 multiple layer을 stack한 모델

  ⇒ different combinations of aggregation functions 이 성능을 향상시킬 수 있음 (dubbed architecture challenge)

• NAS approcah for GNN
  • example: GraphNAS, Auto-GNN: tackle the architeucture challenge
  • approach: design the search space
    • contains all hyperparameters related to GNN models (GraphNAS와 Auto-GNN)
      • 문제1: GeniePath나JK-Network 포함하고 있지 않음 → best performance 보장 x
      • 문제2: architecture search process가 too expensive
  • 본질적인 문제: extremely expensive due to the trial-and-error nature (dubbed computational challenge)
• propose novel NAS framework, which tries to search to aggregate Neighborhood(SANE) for automatic architecture search in GNN
• contribution
  • propose SANE framework based on NAS (emulate more human-designed GNN architectures)
  • for computational challenge, propse differentiable architecture search algorithm
    • trial-and-error based NAS approcah에 비교하여 효율적임
    • first differentitable NAS approach for GNN
    • applicable

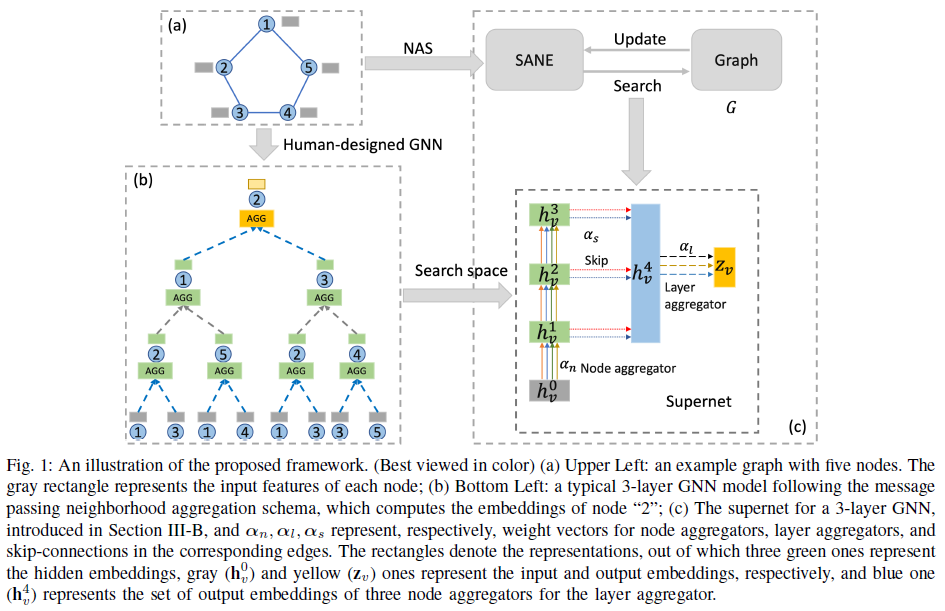
[3. The proposed framework]

[A. The search space design]

• condition for search space
  • large and expressive enough (emulate various existing GNN models)
  • small and compact (compuational resources)
• components

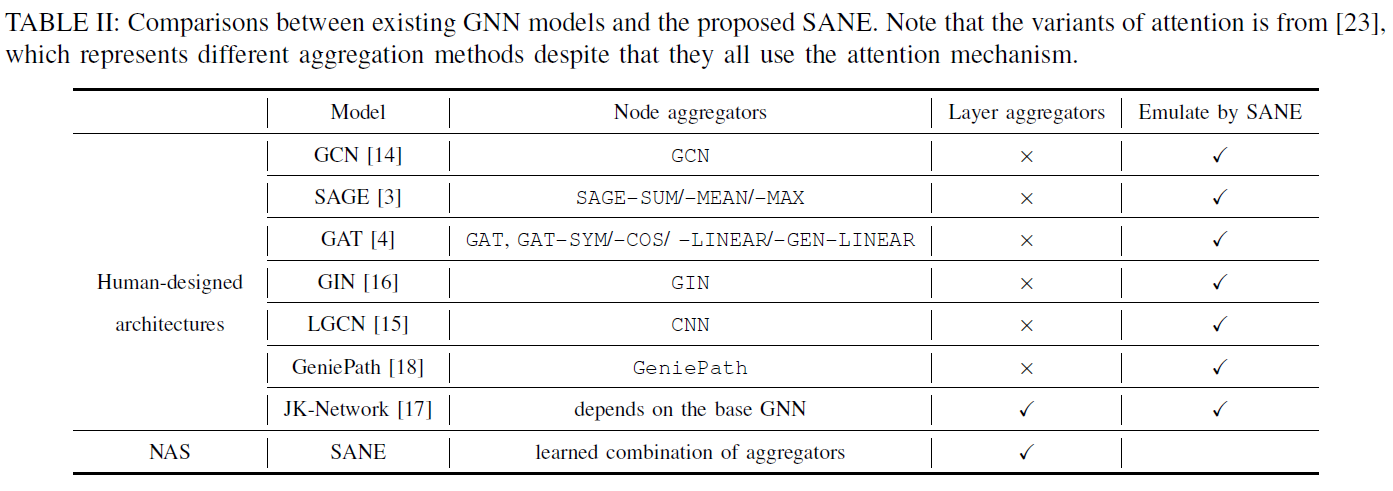
  • node aggregators: $\mathcal{O}_n$ below (11)

    

  • layer aggregators: $\mathcal{O}_l$ above (3) + $\mathcal{O}_s$ (skip-connection) above (2)

  

[B. Differentiable Architecture Search]

• how to represent the search space of SANE as a supernet (DAG in Figure 1(c))

  1) continuous relaxation of the search space

  • Assume we use K-layer GNN with JK-Network as backbone
  • Supernet has K+3 nodes, where each node $x^l$ is a latent representation (ex. input features of node, embeddings in the intermediate layers)
  • each edge associated with an operation $o^{ij}$ (ex. GAT aggreagtor)
  • One input node, one output node, one node representing all skipped intermediate layers ⇒ K+3 node in total
  • task: find proper operation on each edge ⇒ discrete search space에서는 힘듦

  • softmax 를 사용하여 relax

    

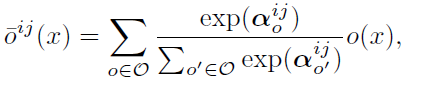
  • $\bar{o}_n, \bar{o}_s, \bar{o}_l$: mixed operations from On, Ol, Os

  • neighborhood aggregation process by SANE

    

  • the mbedding of last layer

    

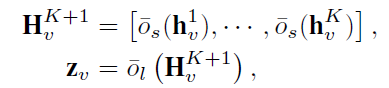
  • after obtain final representation of $z_v$, inject it to different types of loss epending on the given task. i.e. SANE-to solve a bi-level optimization problem:

    

  ⇒ the task of architecture search by SANE=learn three continuous variables $\alpha_n$, $\alpha_s$, $\alpha_l$.

  2) optimization by gradient descent

  

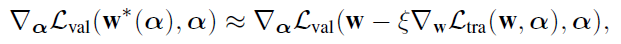
  • instead of obtaining the optimized $w^*(\alpha)$, need to approximate it by adapting w using only a single training step
  • retain top-k strongest operations

  • in the experient, k=1 for simplicity.

    

  

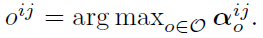
  3) Comparison with Existing NAS methods

  • SANE not include parameters like hidden embedding size, number of attention heads (hyperparameters of GNN models)
  • focus on”aggregation functions”

  

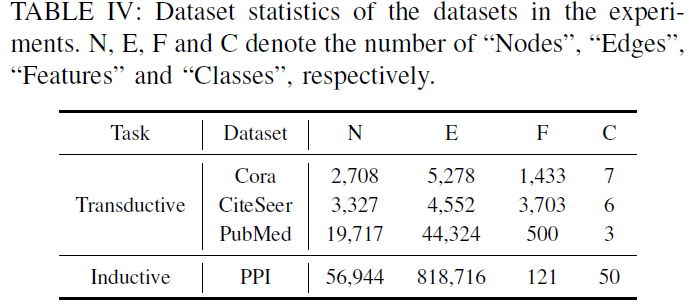
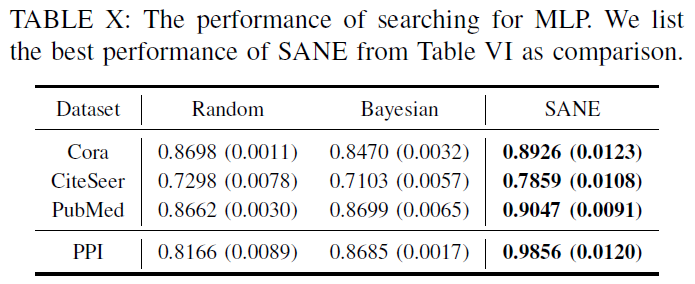
  [4. Experiment]

  

  

  

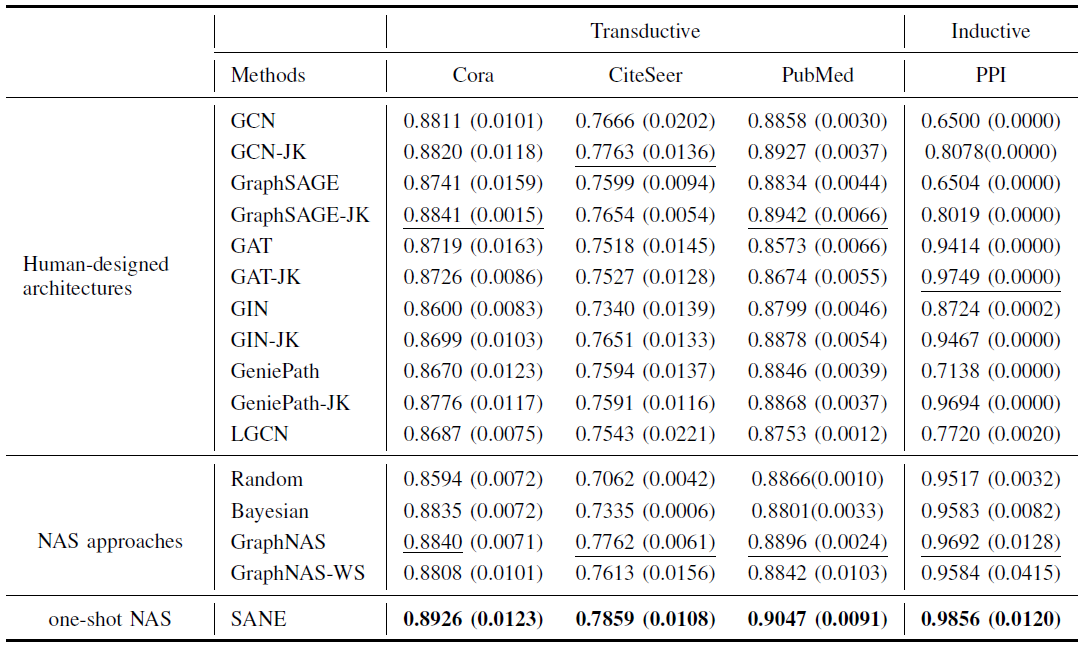
[5. Conclusion]

• propose SANE for graph NAS