[1. Introduction]

  • hypergraph have a main drawback when trying to capture all subleties of these complexes
  • centrality indices: successful tools for discovering structural and dynamical properties of network

[2. preliminaries]

  • adjacent of two simplicies
    • lower adjacent: share a common face (→I think facet..)
    • upper adjacent: two are both faces of the samecommon (k+1)-simplex
      • upper adjacency of 0-simplices :the same as theoretical adjacency
  • family
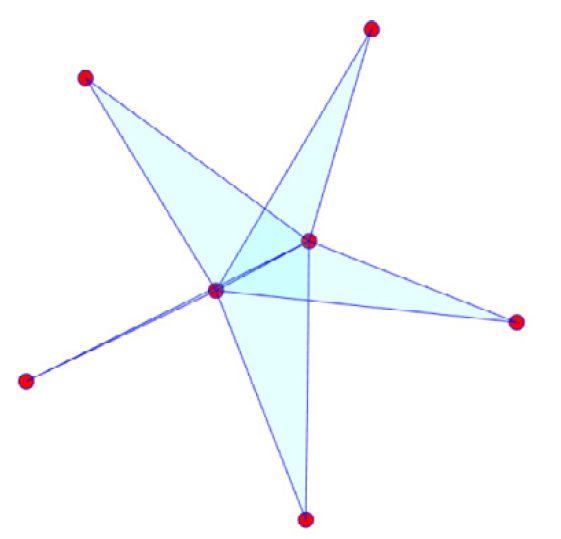
    • $S_l^k$ : consists of a central (k-1)-simplex which is a face of every one of the l k-simplices

      • $S_5^2$

        Untitled

    • $t^k(x_1, x_2, \dots, x_{k+1})$: consists of a central k-simplexes with $x_1$ k-simpliceslower adjacent through one face, $x_2$ k-simplices lower adjacent through another, and so on.
    • $P_l^k$: consist of a k-simplex at one end which is only adjacent to one other k-simplex
      • $P_l^1$: same as the path graph in the traditional network theory

—custom define—

[3. Adjacency matrices in simplicial complexes]

  • use $A_l^k, A_u^k, A_l^k-A_u^k, A_l^k+A_u^k$.
    • sum: emphasize the ffects of the higher simplicial over lower ones
    • difference: indicate two simplices are adjacent or not

  • (two simplices) adjacent: lower adjacent & not upper adjacent

    Untitled

[4 . simplicial shortest distance]

  • $s^k$-walk: sequence of alternating k-simplices and (k-1)-simplices $s_1, e_1, s_2, e_2, \dots, e_{r-1}, s_r$ such that for each $i\in \set{ 1,2,\dots, r-1 }$ $e_i$ is a face of both $s_i$ and $s_{i+1}$, and $s_i$ and $s_{i+1}$ are not both faces of the same (k+1)-simplex.
    • walk on the 0-simplices: walk on the normal graph
  • $s^k$-shortest path: $s_a, e_1, s_2, e_2, \dots, s_n, e_n, s_b$ such that n is minimized
    • proper distance
  • (simplicial complex is) $s^k$-connected: there does not exist a pair of k-simplices $s_a, s_b\in R_k$ where $R_k$ is the set of k-simplices, s.t. $d(s_a, s_b)=\infty$.
    • $s^k$-connected doesn’t mean that it’s $s^{k+1}$-connected or $s^{k-1}$ connected.
  • $s^k$-connected component

  • $s^k$-average simplicial shortest path length:

    Untitled

    • if simplicial complex is not $s^k$-connected, then dealt with component (내가 이해하기론)

  • (lemma)

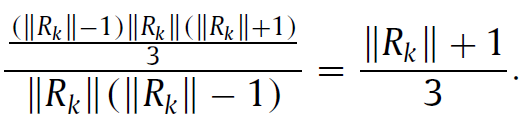
    Untitled

[5. simplicial centralities]

  • degree of a k-simplex : the number of other k-simplices to which s is adjacent
  • $p(\delta_k)$: probability of finding a k-simplex of degree $\delta_k$ in a simplicial complex
  • $P(\delta_k)$: probability of finding a k-simplex of degree larger than or equal to $\delta_k$ in the simplicial complex

⇒ degree distribution of the k-simplices = probability distribution of the degrees of the k-simplices across the whole of simplicial complex

⇒ extends closed centrality concept of Bavelas (1950)

  • simplicial farness: $C(F)=1/\sum_{Y\neq F} d(Y, F)$ (what about infinity?)
  • simplicial harnomic closednesss: $H(F)=\sum_{Y\neq F} 1/d(Y, F)$

  • simplicial betweeness of a k-simplex F: $g(F)=\sum_{S\neq F\neq T} \sigma_{ST}(F)/\sigma_{ST}$ where $\sigma_{ST}$ is the total number of shortest path from S to T and $\sigma_{ST}(F)$ is the number of such paths that pass through F, where $F, S, T\in R_k$.

  • (lemma) adjacency matrix^m gives the number of s^k-walks of length m between k-simplex, i and k-simplex, j

  • simplicial Katzcentrality index

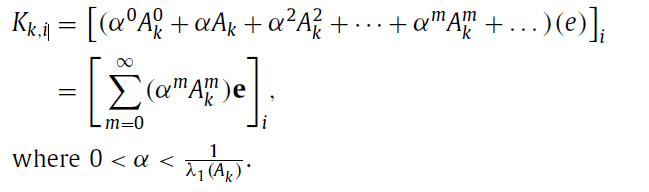
    Untitled

  • simplicial eigenvector centrality

    Untitled