[Abstract]

• propose highly scalable algorithm SSRW (Scalable subgraph Sampling via Random Walk)
• 하나의 고정된 노드 대신 기존에 갔던 노드들의 neighbor에서 새로운 노드를 생성함으로써 graphlet을 sample함
• 4,5,6,7 크기의 graphlet까지 counting 완료

[3. The Scalable Subgraph Sampling Algorithm]

• when a random walk get mixing, every node in the random walk serves as a starting node and induces a k-subgraph with our sampling strategy

[3.1 Sampling Strategy for k-Subgraphs]

• first choose 2-path
• for $3\leq t\leq k$, the t-th node $v_t$ is selcted from the neighbors from the previous t-2 nodes (all except for the first one)

• note: lline 3 is a multiset, not the union (helps to make unbias estimation)
• Theorem 1: Algorithm 1 generates all k-graphlets in graph G for $k\geq 2$

[3.2 Computation of Repeat Coefficient]

• A k-tuple can be generated through various ways

  

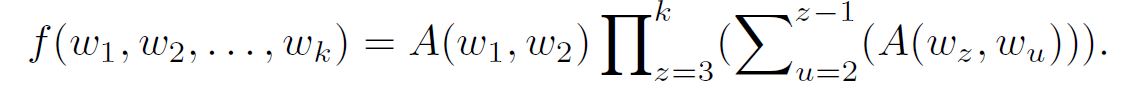
[3.3 Unbiased Estimator]

• When a random walk get mixed, the probability of the appearance of node v is P(v)=d(v)/D, where D is the sum of degrees of all nodes in G
• The sequence $r^{(k)}=(v_1, v_2, \cdots, v_k)$ is genrated with probability

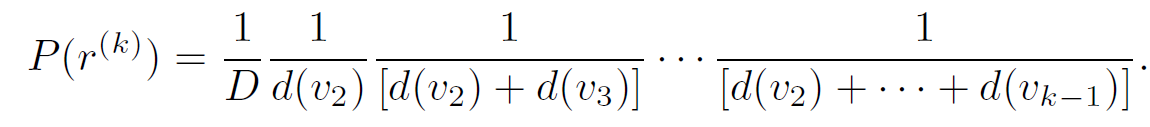
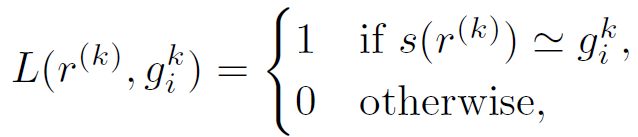
• Theorem 2: The unbiased estimator for $C^k_i$, the count of graphlet $g_i^k$, is $\hat{C}i^k=\frac{1}{n\alpha_i^k}\sum{i=1}^n \frac{L(r^{(k)}, g_i^k)}{P(r^{(k)})}$

⇒ can get counts