[Abstract]

  • sample synthetic networks that preserve the d-hop neighborhood structure
  • employ a colored configuration model (color refinement algorithm)
  • generated synthetic networks and the original network becomes similar (centrality measures : PR, HITS etc.)

Untitled

[Introduction]

  • Sampling networks with predefined properties
  • limitations
    • merely preserve local information
      • node degrees, simple global network statistics
      • ER, configuration models
    • preserve certain meso cale structures and motifs, but not scalable
      • exponential random graph
  • introduce “NeSt” models
    • preserve mesoscale network structure
      • neighborhood trees
      • well-approximate centrality measures
    • efficiently sample
    • combine Color Refinement or Weisfeiler0Lehman algorithm with a locally Colored Configuration model
    • hyperparameter: depth d → tune how eep the multi-hope neighborhood structure of each node in the original network is preserved in the null model
  • contribution: introduce $NeST^d_G (c^{(0)})$ model
    • prove NeST samples exactly preserve popular centrality measure of G for an appropriate choice of $c^{(0)}$ and large d
  • random graph
    • ER: preserves network density on expectation
    • Configuration model: degree of each node
    • ERGMs: specify structures to be preserved in expectation
    • Machine learning based network generators

[2. Preliminaries and Notations]

  • coloring
    • c1 refines c2 if c1(v)=c1(u) implies c2(v)=c2(u)
    • c1 refines c2 and vice versa ⇒ c1 equals to c2
  • centrality measures
    • assign importance scores to nodes
    • this paper focuses on “eigenvector-based centralities”

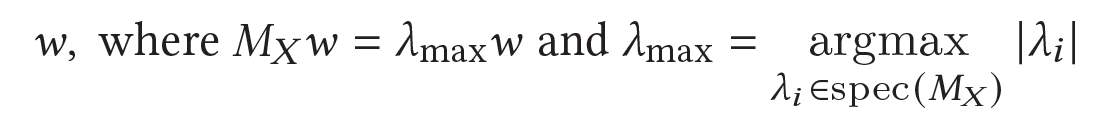
    Untitled

[2.1 Color refinement]

  • from initial coloring $c^{(0)}$, the colors are updated by distinguishing nodes that have a different number of colored neighbors
  • stop when no changes occur

  • CR procedure:

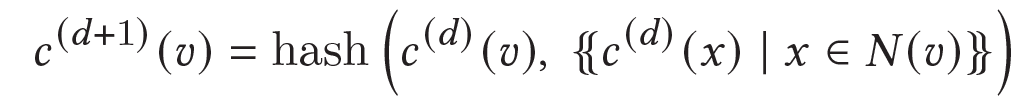
    Untitled

    • hash: injective function from a pair onto a color space
    • the colorings are iteratively refined
    • once a stable partition is reached, the partition will not change
      • the nodes’ colors induce an equitable partition (all nodes within one class have the same number of connections to another class)

    • extension for directed graphs

      Untitled

[3. The NeST Model]

  • NeSt = Neighborhood Structure Configuration model
  • preserves neighborhood structure information of an orignal network up to a specific depth d as encoded with the Color Refinement Algorithm
  • easy to fit and sample
  • hyperparameter: $c^{(0)}$ and d
    • preserving the neighborhood tree structure at depth d also preserves the neighborhood structure at depth $d’\leq d$

  • noteworthy properties

    Untitled

    • $N_G^{(d)}(const)$ implies coloring all nodes with the same color

[3.1 Sampling from the NeSt model]

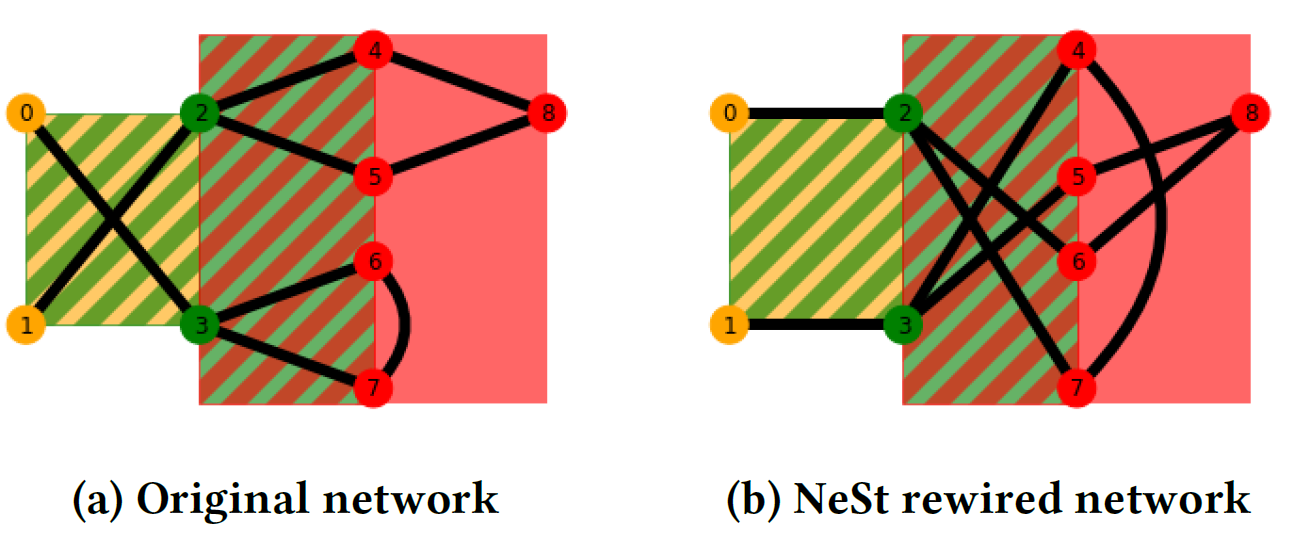
Untitled

  1. partition the edges according to the colors of their endpoints
    • ex) $g_{green, red}$
    • for directed graphs, $g_{green, red}$ and $g_{red, green}$ are different
  2. randomize each subgraph via edge swaps
    • choose two edges at random and swap their endpoints with one another
    • rewired as a bipartite configuration model - sampling
    • MCMC
    • other strategies are also fine

Untitled

⇒ CR iteration doesn’t change colors

  • Algorithm 1
    • rewiring each subgraph independent one another

Untitled

  • Algorithm 2
    • perform randomization one flip at a time
    • more similar to other MCMCs

Untitled

[3.2 Variations of the NeSt model]

  • initial node colors
    • if network is bipartite → reflect bipartition
    • if network comprises several components → reflect the component
    • if want to preserve PR → color our graph with the out-degree of the nodes
  • incorporating externally defined node colors (predefined colors)
    • only direct node neighboros are additionally identfied by their external color, while two-hop neighbors are not
  • samples in between depth d and d+1

[4. The role of the depth parameter d]

[4.1 Maximum depth preserves centralities exactly]

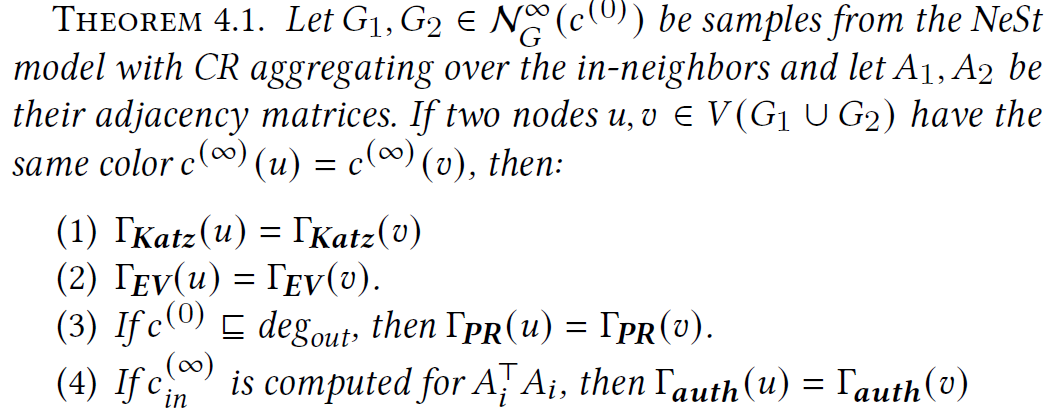
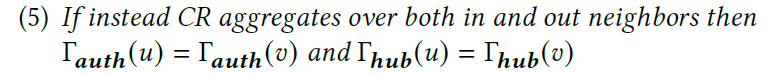
Untitled

Untitled

[4.2 Intermediated approximates centralities]

  • preserving smaller neighborhood depths is already sufficient

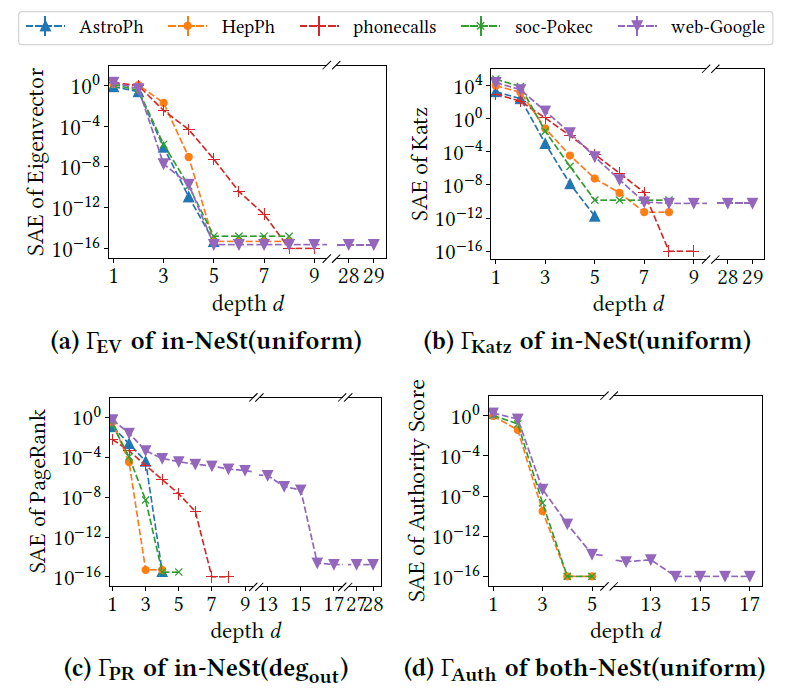
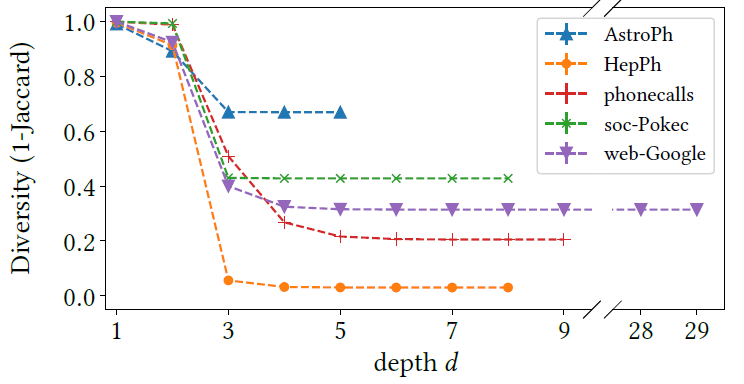
Untitled

Untitled

[5. Empeirical Illustration]

  • NeST has smaller SAE, Jaccard similarity, rewire time compared to ER and ERGM.

[6. Discussion]

  • preserving centralities
    • focus: presrving centralities « maintaining neighborhood tree structure
  • limiting the number of colors

[7. Conclusion]

  • relationship with GNN
    • undesirable to distinguish nodes with 1000 and 10001 neighbors