[Abstract]

• fundamental task for KGs = KGC

  ⇒ predict unseen edges

  • concern: degree bias
    • poor representations for lower-degree nodes
      1. validate the existence of degree bias
      2. identify the key factor to degree bias
      3. novel data augmentation model, KG-Mixup to generate synthetic triples to mitigate such bias

[1. Introduction]

• KG: each edge represents a single fact (h, r, t)
  • h, t, r: head, tail, relation
• problems: degree bias

  • validation: graph classification, link prediction tasks for homogeneous graphs

    ⇒ However, KGs are naturally heterogeneous

• questions: whether degree bias exists in KGs and how it affects the model performance in the context of KGC?
• in-degree of entity t: #triples where t is the tail entity
• tail-relation degree: #triples where t and r co-occur
• when predicting t, #triples where entity t and relation r co-occur as an entity-relation pair correlates significantly with performance
  • ex) for figure 1, it is hard to predict “Germany”, which has a tail-relation degree of one

[2. Related Work]

• KG embedding: TransEm, ConvE, R-GCN
• Imbalanaced / Long-Tail Learning (class distribution is highly uneven): SMOTE
• Degree bias
  • some works dealt with degree bias in KGs, proposing debaising methos that utilizes random graphs
  • no work that focuses on how the intersection of entity and relation degree bias effects embedding-based KGC
• data augmentation for graphs
  • few for augmenting KGs

[3. Preliminary Study]

• embedding method : ConvE, TuckER
• embedding for a node v, a relation r
• focus on predicting the tail entity (since its equivalent)

(1) Does degree bias exist?

(2) Which factor in a triple is related to such bias?

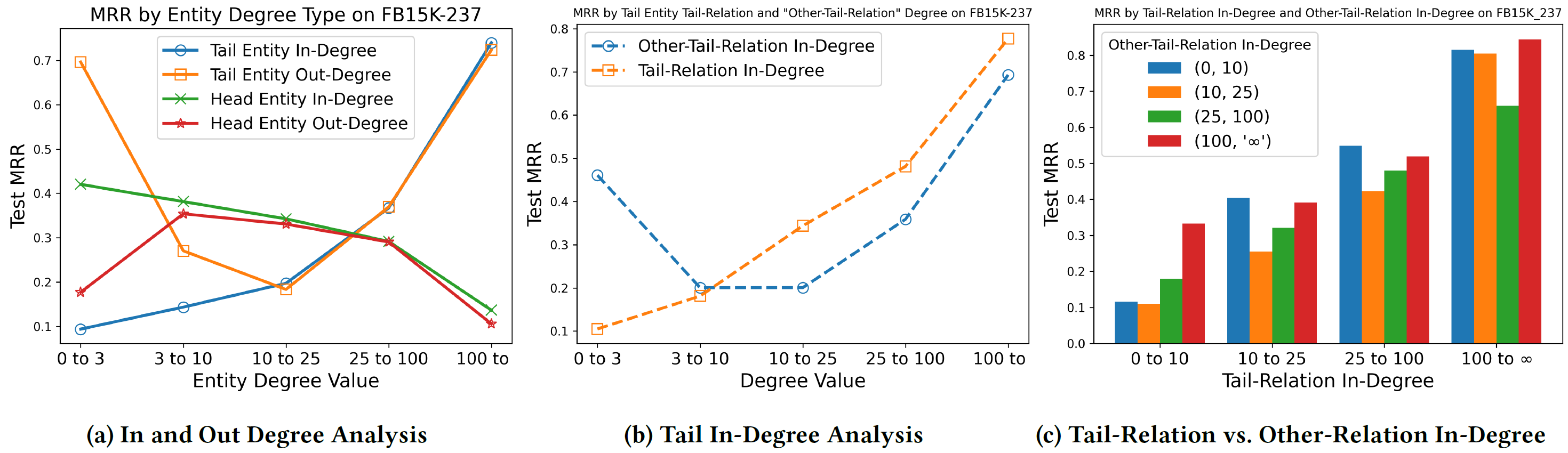
[3.1 Entity Degree Analysis]

• measure: mean reciprocal rank (MPR)

(1) tails’ degree has a larger impact on test performance than head’s

(2) tail in-degree features are more distinguishing and apparent relationship with performance than the tail out-degree

[3.2 Entity-Relation Degree Analysis]

• how both relation and etities in a triple together impact the KGC performance?
• definitions

  • the relation-specific degree:

    

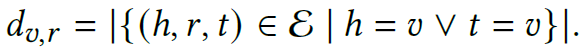
  • the tail-relation degree

    

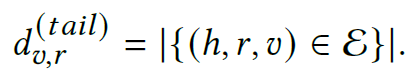
  • other-tail relation degree

    

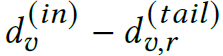
• While both (tail-relation, other-tail relation) correlate with performance, the performance when the other-tail-relation degree in the range [0,3) is quite high

  ⇒ Which one is the dominant factor?

  ⇒ Tail-relation (small variance on Figure 2(c))

• difference between prior studies
  • This paper focuses on “frequency among entity-relation pairs” while other concentrate on just degree

[4. The proposed method]

• propose method for improving the KGC performance of triples with low tail-relation degrees (KG-Mixup)
  • augmenting the low tail-relation degree triples during training with synethetic samples

[4.1 General Problem]

• create synthetic triples for those entity-relations pairs with a low tail-relation degree
  • n: the upper bound for tail-relation degree
  • k: #synthetic amples

  

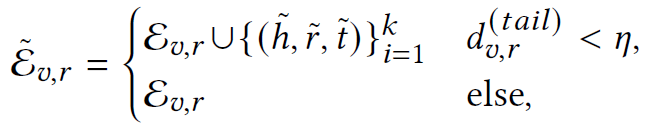
• challenges
  • diversity of synthetic samples
  • computational costs

[4.2 KG-Mixup]

• tackles
  • nonexistence of a label of each triple ⇒ consider t1 as a label
  • mixing criteria ⇒ mix other triples that share the same tail and distinct h,r

  • how to mix?

    

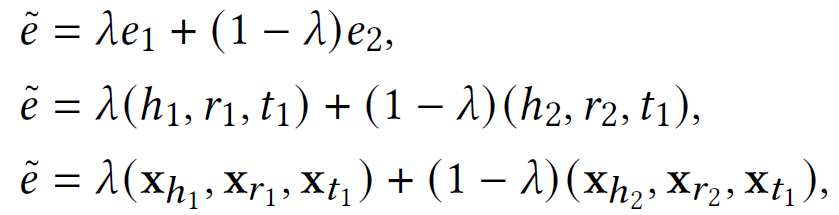
  [4.3 KG-Mixup Algorithm for KGC]

  

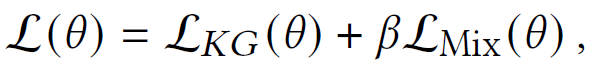
  • loss on KG triples and synthetic samples

[4.4 Algorithmic Complexity]

• $O(N\abs{E}O(f))$

[5. Regularizing effect of KG-Mixup]

[6. Experiments]

• baseline
  • over-sampling
  • loss re-weighting: assign a higher loss ti triples with a low tail-relation deree
  • focal loss: a higher weight to misclassified samples