[Abstract]

• Hypergraph clustering
• O(log n) approximate algorithm for hypergraph ratio cut
• significantly faster than existing hypergraph ratio cut algorithms

[1. Introduction]

• minimize a ratio cut objective (ratio between the cluster’s cut and some notion of the cluster’s size)
• challenge to hypergraph
  • more than one way to partition a hypergraph

  ⇒ notion of a generalized hypergraph cut function

• previous work and limitations
  • extension to hypergraphs
    • notions of graph laplacian operators are nonlinear → computational cost
    • obtaining guarantees for generalized hypergraph cut function
  • hypergraph algorithms
    • theoretical O(n3)
    • confined to simple notion of a hypergraph cut function
    • recent techniques come with practical implmentation, not providing theoretical guarantees
  • present work
    • practical and general approximation algorithms for hypergraph ratio cuts
    • worst-case O(log n) approximation
    • applies to any cardinality-based submodular hypergraph cut function and any positive node weight function

[2. Preliminaries and related work]

• boundary of S

  

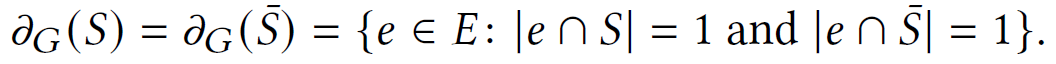
• cut(S)

• ratio cut objective

  

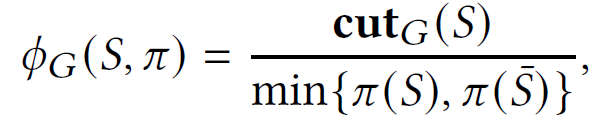
  • capture conductance when $\pi(u)=d_u$
  • capture expansion when $\pi(u)=1$

• $\pi$ -expansion of a graph G

  

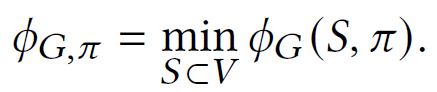
• a graph is known as an expander graph if its expansion < c
• can be extended to directed graphs

[2.1 Graph flows]

• a nonegative flow value f(ij) to each (i,j)
  • if f(i,j) ≤ w(i,j), then f satisfies capacity constraints

  

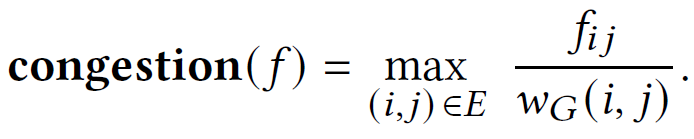
• satisfies flow constraints at a node v if flow into v == flow out of v
  • out > in (deficit), in > out (excess)
• definition
  • s-t flow
  • multicommodity flow

[2.2 General hypergraph cuts and expansion]

• boundary

  

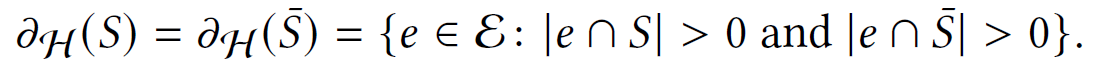
• all-or-nothing hypergraph cut function

  

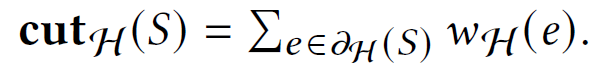
• generalized hypergraph cut

  

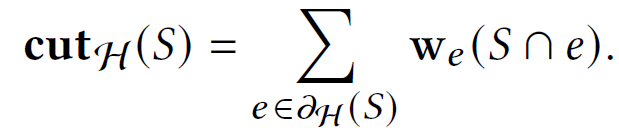
  • each hyperedge e is associated with a splitting function $w_e : A\subset e \rightarrow \mathbb{R}$ that assigns a penalty for each way of seperating the nodes of a hyperedge

  • axioms

    

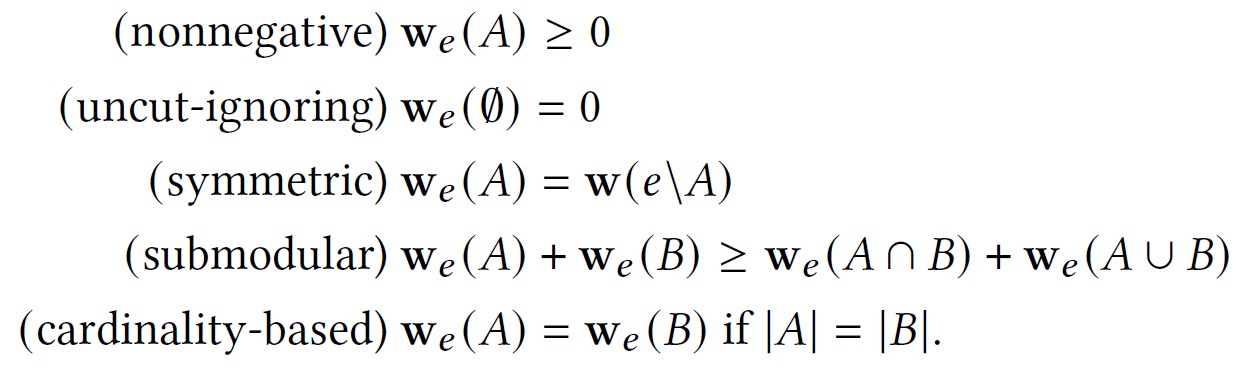
    ⇒ if satisfied, $cut_H$ is a cardinality-based submodular hypergraph cut function

• generalized hypergraph cut expansion

  • given: a hypergraph, node weight function, generalized hypergraph cut function

  • the hypergraph $\pi$ -expansion of a set $S\subset V$:

    

    

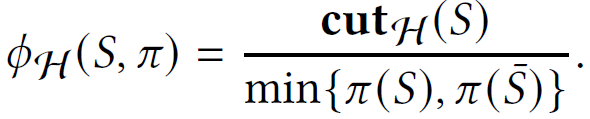
[3. Hypergraph expander embeddings]

[3.1 Hypergraph cut preservers]

• employ reducing a hypergraph to a graph

  

  

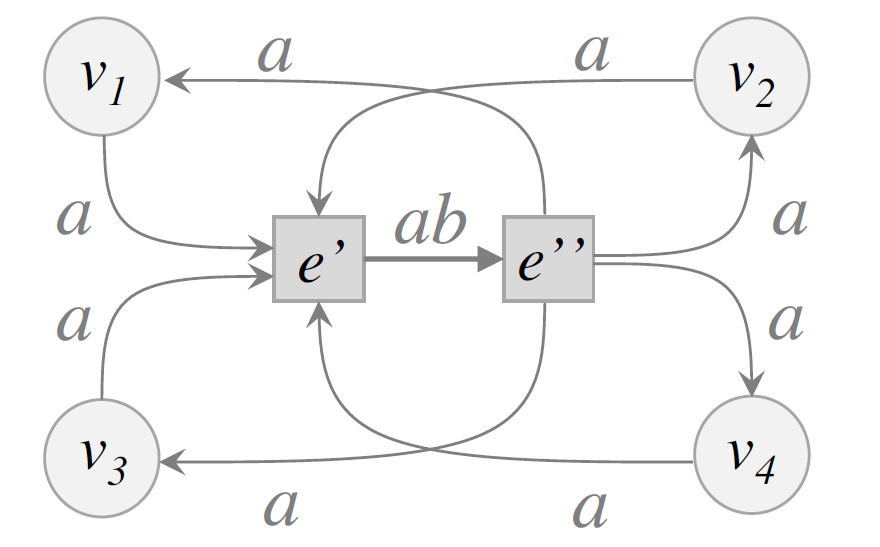
  ⇒ not unique method of constructing an augmented cut preserver for a cardinality-based submodular hypergraph cut function

[3.2 Expander embeddings in directed graphs]

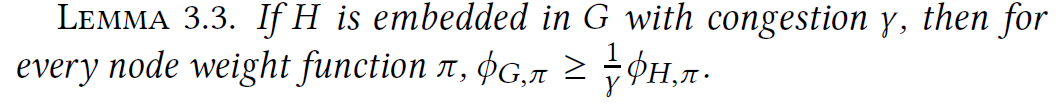
[3.3 Hypergraph expander embeddings]

• combine hypergraph cut preservers + definition 3.2

  

[4. Hypergraph flow embedding]

• to apply lemma 3.4, embed an expander into G(H) with a small congestion

[4.1 Maximum flows in an auxiliary graph]

• fix a>0 and a partition ${R, \bar{R}}$ satisfying $\pi (R)\leq \pi (\bar{R})$, and set $n = \pi (R)/\pi (\bar{R})$
• solve maximum s-t flow problem on an auxiliary graph G(H, R, a)

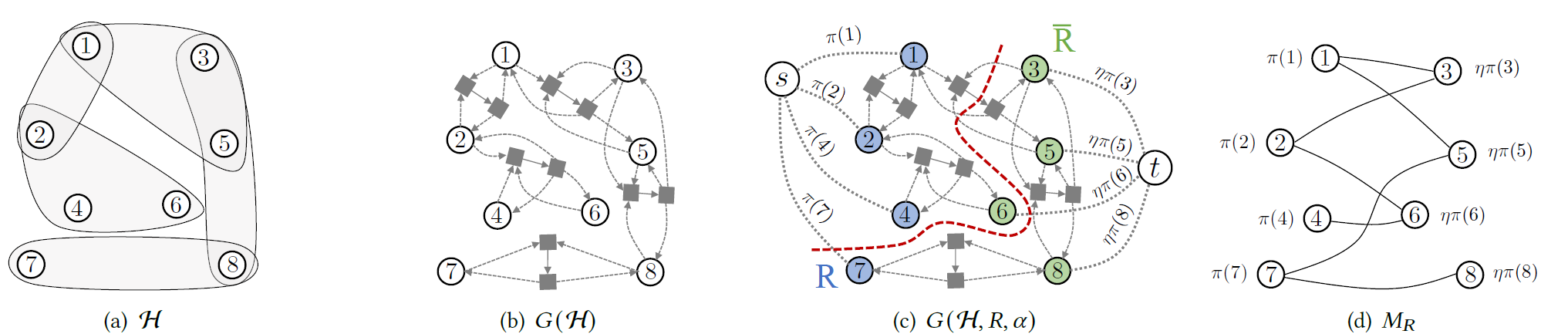
• find a set S with small expansion, or find an embeddable bipartite graph btw $R, \bar{R}$ with congiestion 1/a

• minimum s-t cut problem in G(H, R, a) = solving the following optimization problem

  

  

  

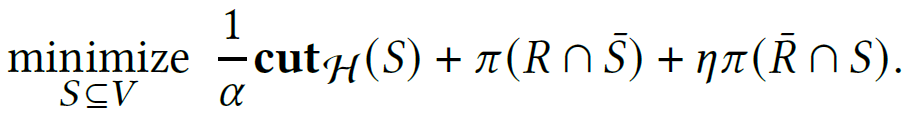
[4.2 The flow-embedding algorithm]

• Algorithm 1: obtain both a good cut and an embeddable bipartite graph for any input parition ${R, \bar{R}}$ satisfying $\pi (R)\leq \pi (\bar{R})$

  

  

[5 Hypergraph ratio cut algorithms]

[5.1 Expander building subroutines]

• each iteration
  • cut player : produce a bisection Rs
  • matching player: produces a fractional perfect matching $M\in [0,1]^{\abs{V}\times \abs{V}}$ between Rs
• union of maching defines a graph $H_t = \bigcup_{j=1}^t M_j$ with adjacency matrix $A_t=\sum_{j=1}^t M_j$
• goal: choose bisections minimizing the number of rounds it takes before Ht is an expander

[5.2 The approximation algorithm]

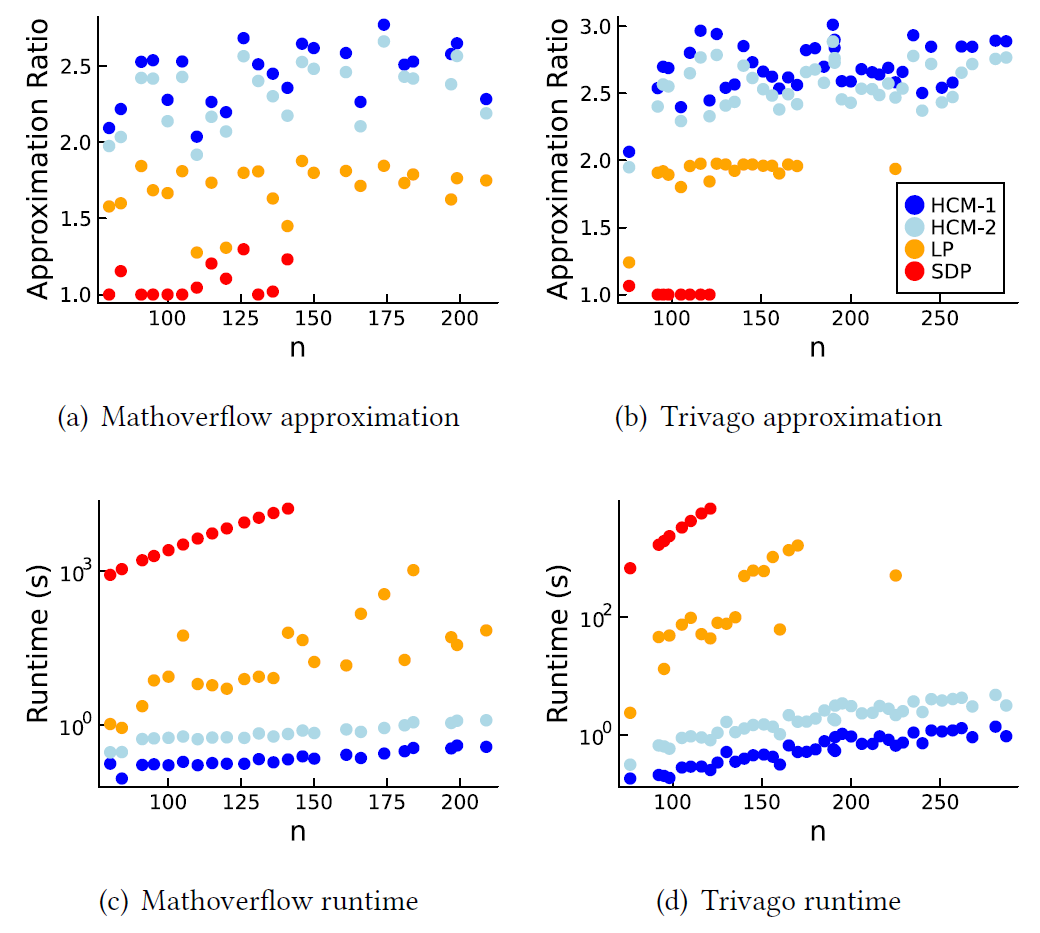
[6. Experiments]

[7. Discussion]

• explore best generalized hypergraph cut functions
• find improved approximation algorithmbeyond cardinality based