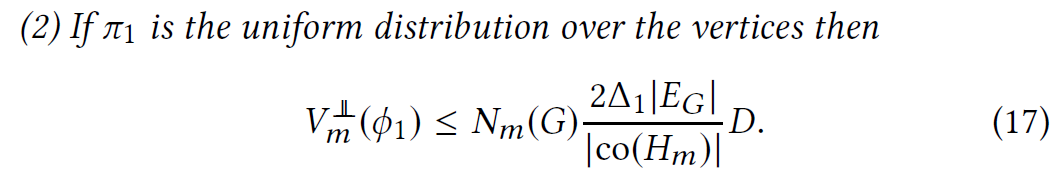[Abstract]

• introduce a MC sampling technique for graphlet counts (Lifting)
• variants of lifted graphlet counts, including ordered, unordered, and shotgun estimators, random walk starts, and parallel vertex starts

[1. Introduction]

• propose a class of MC sampling method called lifting
• MC sampling perform random walk on graphlets → only require local graph information → memory efficient
  • GUISE
  • PSRW
  • waddling random walk (have not been extended k≥5)

[1.1 Our contributions]

• propose
  • ordered lift estimator
    • allows shotgun sampling (sample subgraphs in one shot)
    • unbiased
    • variance: $\Delta^{k-2}$
  • unordered lift estimator

[2. Sampling Graphlets]

[2.1 Definitions and notation]

• $N_e(S)$: the set of all edges that connect a vertex from S and a vertex outside of S
• $deg(S)=\abs{N_e(S)}$
• $deg_S(u)$: the number of vertices from S that are connected to u

⇒ $deg(S)+2\abs{E_S}=\sum_{v\in V_S} deg(v)$

[2.2 Prior graphlet sampling methods]

• uniform sampling → imposible

• use Horvitz-Thompson inverse probability weighting

  

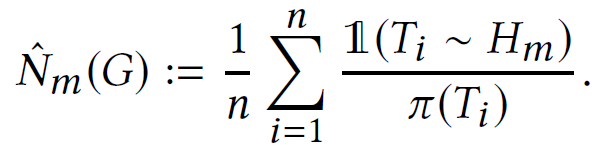
• PSRW
  • SRW: construct CIS-relationship graph and random walk
    • edge: sampled with equal probability
  • PSRW: modification of SRW algorithm

  ⇒ insufficient mixing → cause biasedness

  ⇒ mixing time can be of order $O(n^{k-2})$

• naive RW on G
  • cannot sample certain graphlets (e.g. stars)

  ⇒ SRW on CIS of size k-l+1 ⇒ slow mixing, and need to calculate global constants

• Waddling protocol
  • retains a memory of the last s vertices and extends this subgraph by k-s vertices from either the first or last vertex visited in the s-subgraph

  ⇒ depend on desired graphlet

  ⇒ involves a rejection step

• lifting
  • requires little tuning, never reject graphlets

[3. Subgraph Lifting]

• attach a vertex to a given CIS
• for any (k-1)-CIS, S, we lift it to a k-subgraph by adding a vertex from its neighborhood, $N_v(S)$ according to some probability distribution
• at each step, sample $(v_i, v_{r+1})$ from $N_e(S_r)$ uniformly at random
• lifting and waddling: inherit the mixing time of a simple random walk by initializing with the stationary distribution

[3.1 Unordered lift estimator]

• ignore the order of nodes visiting in the graphlet
• probabilitly is a function of only degrees of vertices $V_T$

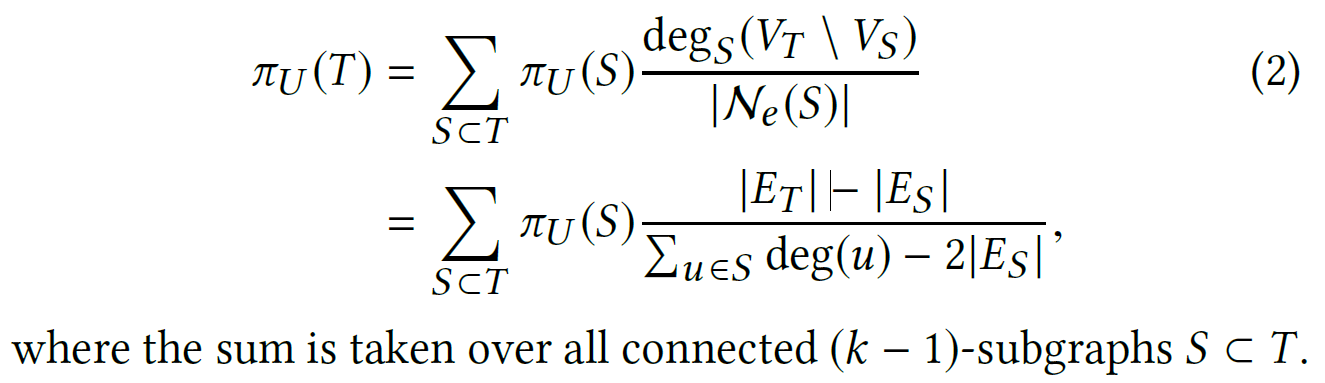
• co(T): certain ordering of vertices in T

  

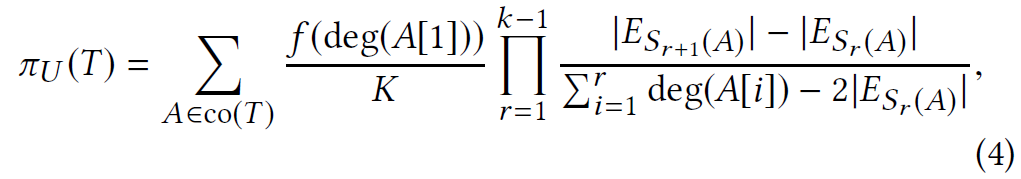
  since it is a function of degree,

  

  We just need to precompute it for all T

[3.2 Ordered lift estimator]

• maintain the ordering of the vertices

  

  

  

  

  

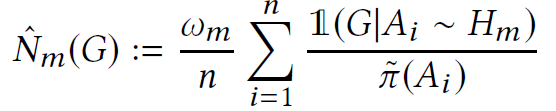
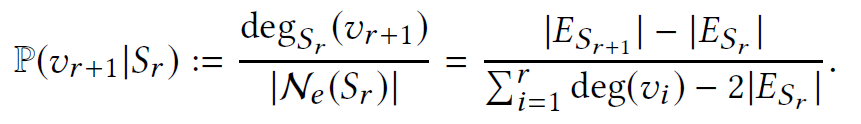
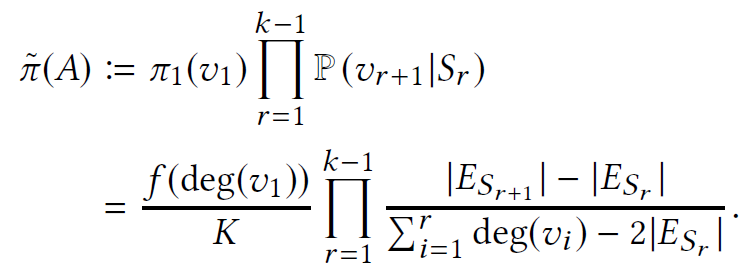
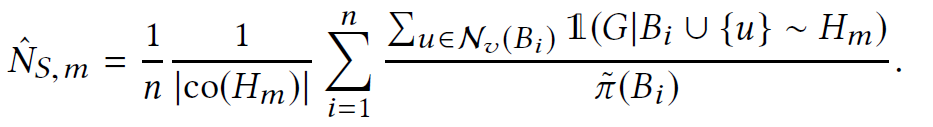
  • shotgun sampling: to incorporate information about all k-CISs in the neighborhood of Bi

  

  

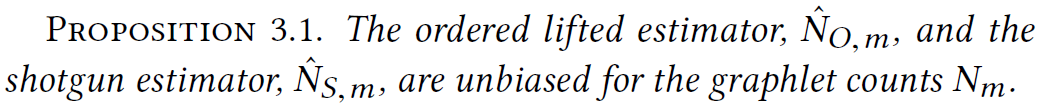
[4. Lifting Variance]

• consider two methods
  • uniform selection over the set of vertices
  • random walk on the vertices

  

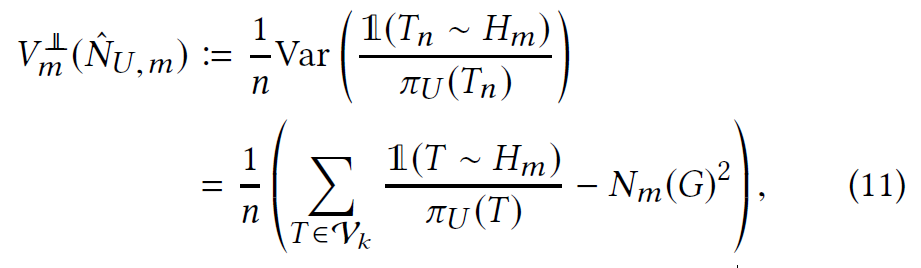
[4.1 Theoretical variance bound]