[Abstract]

  • generate synthetic graph that matches properties

    ⇒ propose to use Kronecker graphs: KronFit

    • takes linear time

[1. Introduction]

  • a graph generation model would like
    • obey many properties as possible
    • parmeter fitting should be fast and scalable
    • resulting set of parameters should generate realistic-looking graphs
  • benetifs and applications
    • give information about the structure of graph itself
    • graph compression
    • extrapolations
    • sampling
    • anonymization

[2. Related Work and Background]

  • graph patterns
    • power-law degree distribution
    • small diameter
  • generative moel
    • Erdos-Renyi → fails to generate power-law degree distributions
    • Watts & Strogatz → small diameters
    • preferential attachment → power-law + low diameters
      • variations
        • copying model
        • winner does not take all
        • forest fire

      ⇒ Only single property is preserved

  • Fitting graph models

[3. Kronecker Graphs]

  • recursive construction
  • Kronecker product of graph adjacency matrices

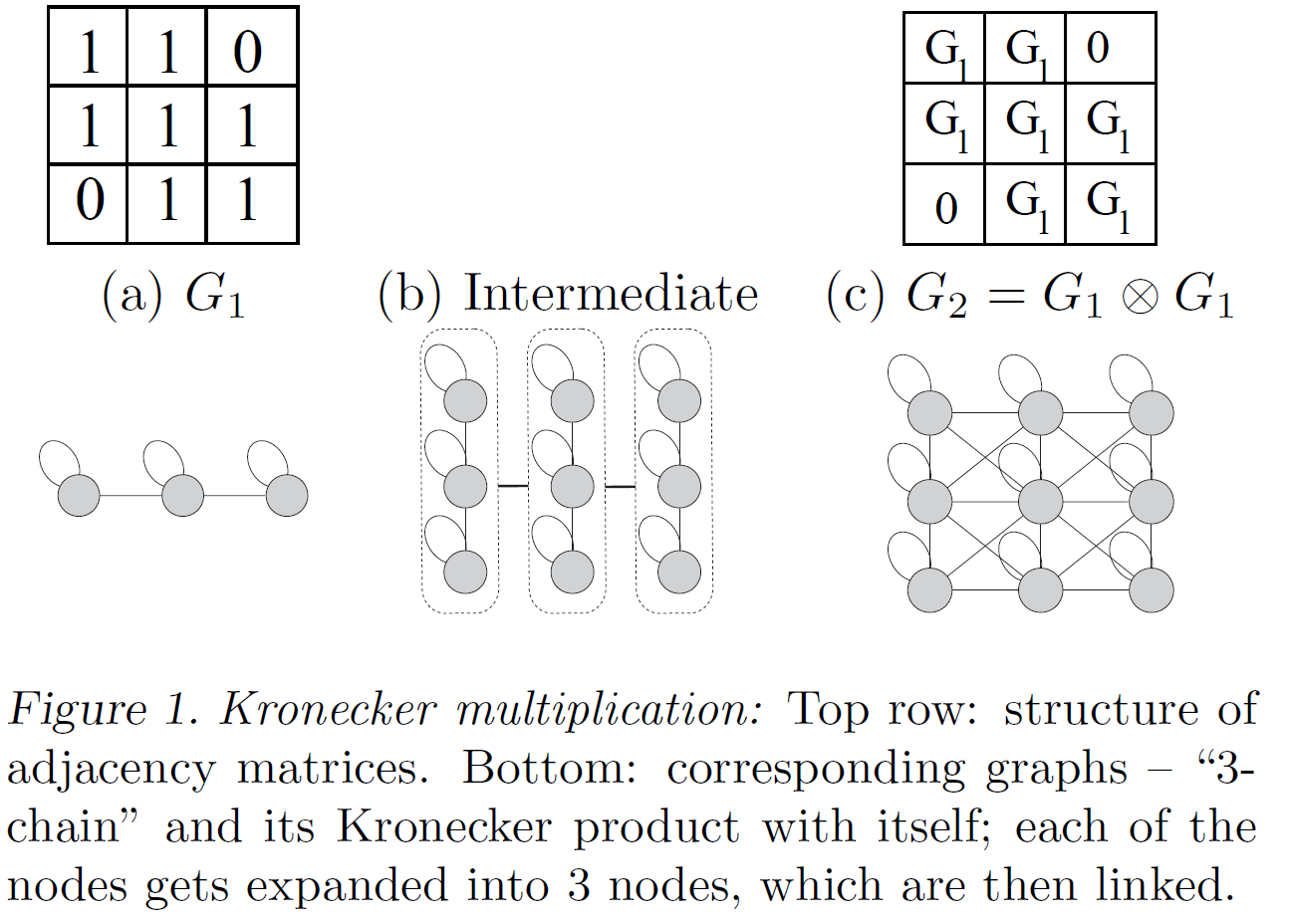
Untitled

Untitled

  • Stochastic Kronecker Graphs

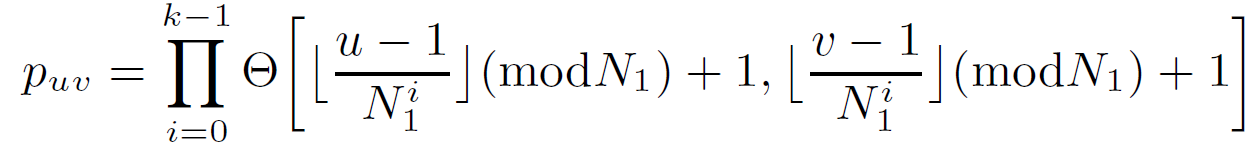
    Untitled

[4. Proposed Method]

[4.1 Preliminaries]

  • P(G): likelihood that a given model generated graph G
  • adopt maximum likelihood approach
    • find $\Theta$ that maximize the $P(G)$
  • challenges
    • model selection
    • node labeling (ordering)
    • likelihood estimation $P(G;\sigma)$ takes $O(n^2)$

    ⇒ sampling to avoid super-exponential sum over the node labelings. develop an algorithm to evaluate $P(G;\sigma)$ in linear time $O(E)$

[4.2 Problem Formulation]

  • to solve: $\arg\max_\Theta P(G;\Theta)$

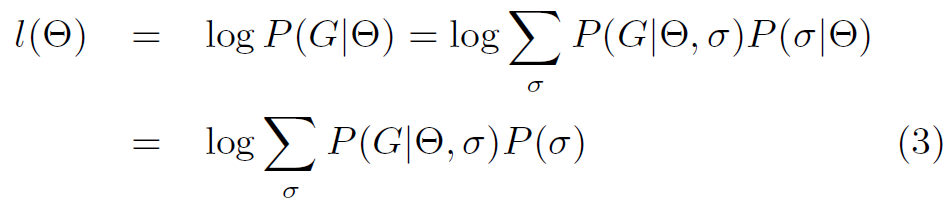
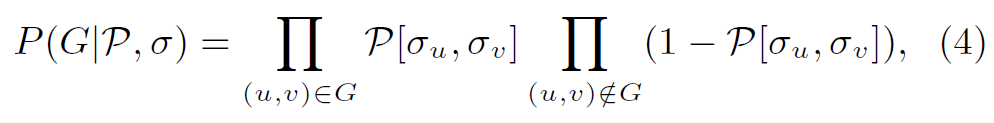
    Untitled

    Untitled

    • identically, compute $l(G;\theta)$ and the gradient matrix $\partial l(\hat{\Theta}_t)/\partial \hat{\Theta}_t$ and update using the gradient

      ⇒ problem: assumption of (almost) nonexistence of local minima, too many permutations, (4) takes $O(N^2N!)$

[4.3 Summing over the Node Labelings]

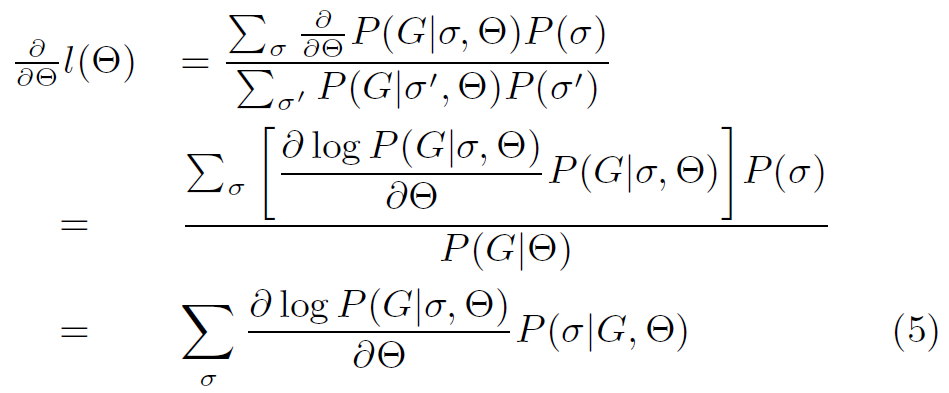
Untitled

⇒ still need summing over all permutations → use Metropolis algorithm to simulate draws from the permutation distribution (ref: https://rooney-song.tistory.com/26)

use sampling for calculating gradient

use sampling for calculating gradient

Untitled

[4.4 Efficiently Evaluating the Likelihood]

  • Algorithm 2: $l_t$

  • taylor expansion

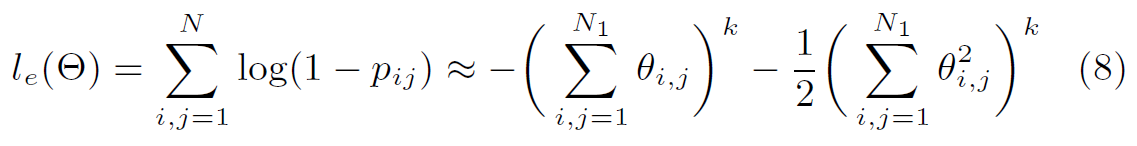
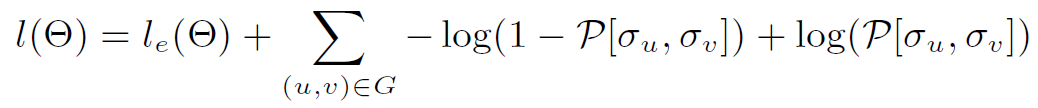
    Untitled

    Untitled

[4.5 Determining Size of the Initiator Matrix]

  • propose to use BIC

[5. Experiments]

Untitled