[Abstract]

• propose MAG model, that captures the interactions between the network structure and the node attributes

[1. Introduction]

• questions
  1. real graph가 어떻게 생겼는가?
  2. observed patterns를 설명할 수 있는 모델을 어떻게 찾을 수 있는가?
  3. 모델의 알고리즘 결과가 어떠한가?
• emprical analysis of large real-world networks: heavy-tailed degree distributions, local clustering of edges, small diameter
• model design
  • preferential attachment
• mechanistic vs statiscal
  • mechanistic: emphsize structural properties → not lend themselves to model parameter estimation
  • statistical: network properties do not naturally emerge from the model in general

  ⇒ Kronecker graphs model both satisfy this

  • use only 4 parmeters
  • accurately model the global structural properties
    • degree distribution
    • edge clustering
    • diameter and spectral properties
• Modeling networks with rich node attribute information
  • interaction: network structure + node attributes
  • questions
    • node의 heterogeneity를 어떻게 고려할 것인지
    • node feature를 edge probabilities를 얻을 때 어떻게 활용할 수 있을 것인지

    

    ⇒ propose Multiplicative Attribute Graphs (MAG)

    • consider a model where each node is a vector of categorical attributes
    • reflect homophily and heterophily (both naturally occur in social networks)
• flow
  • show the model obeys densification power law
  • connectivity of MAG model
  • diameter is small
  • log-normal degree distribution

[2. Formulation of the Multiplicative Attribute Graph Model]

• general considerations
  • node: categorical attributes
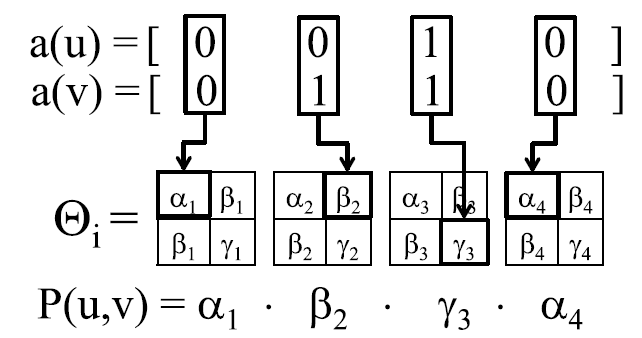
  • $\theta_i$: each attribute-attribute similarity matrix
    • represent the probability of an edge given the values of the i-th attribute of both nodes
    • if attribute reflects homophily → diagonal value high
    • if attribute reflects heterophily → off-diagonal value high

• The Multiplicative Attributes Graph (MAG) model

  $P[u,v]=\prod_{i=1}^l \Theta_i[a_i(u), a_i(v)]$

  • how can estimate of matrices $\Theta_i$?

    ⇒ this paper focus on mathematical analysis

• Simplified version of the model
  • directed → undirected (for symmetry)
  • binary node attributes (2*2 matrices)
  • reduce #parameters ($\Theta_i=\Theta, \forall i$)
    • all entries are between 0 and 1
    • assume $\Theta[1,1]>\Theta[1,0]=\Theta[0,1]>\Theta[0,0]$ (natural property: core-periphery)
  • assume a simple generative model of node attributes

    • i.i.d Bernoulli distribution

      $P(a_i(u)=1)=\mu$ for $i=1,2,\dots, l$ and $0<\mu<1$

  ⇒ MAG model : $M(n, l, \mu, \Theta)$

  • study properties resulted from this
• Connections to other models
  • Latent Space Model
    • probability of an edge: euclidean distance between the nodes
  • Random Dot Product
    • inner product of nodes
  • Multifractal Network Generator
    • special case of MAG: node attribute distribution, similarity matrix are equal for every attribute

  • MAG generalizes Kronecker graphs

    

[3. The Number of Edges]

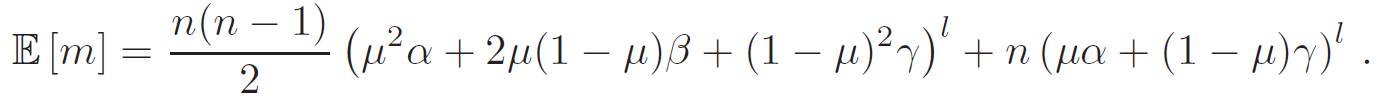
[4. Conectivity]

• MAG model obeys the Densification Power Law

[5. Diameter]

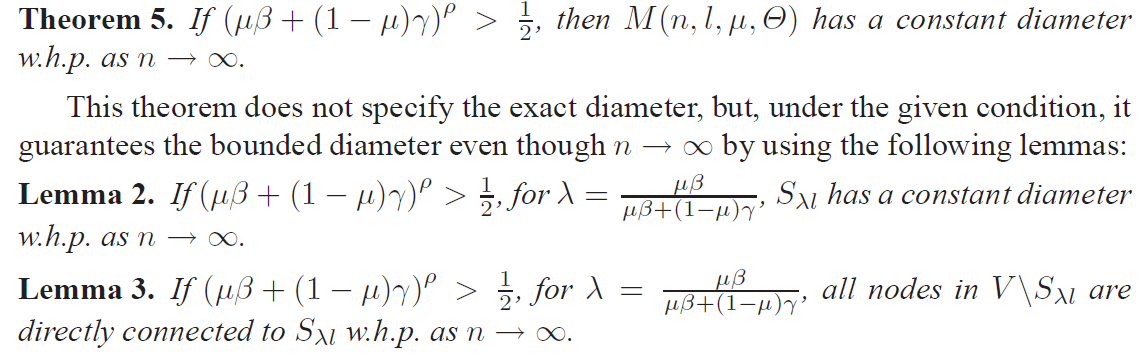
• diameter of the network remains small

[6. Degree Distribiution]

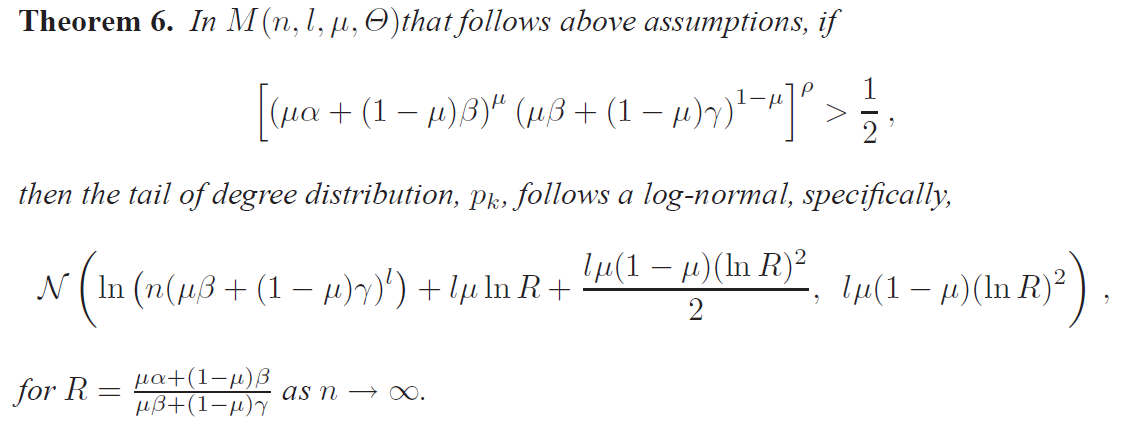
• the degree distribution of MAG model apprxoimately follows a quadratic relationship on log-log scale