[Abstract]

• generating privacy-preserving graph data
• transmitting privacy-preserved information

[1. Introduction]

focus on

1. privacy-preserving graph data

   • how can we protect (mask, hide, perturb) sensitive information from node identify disclosure and link re-identification?

     

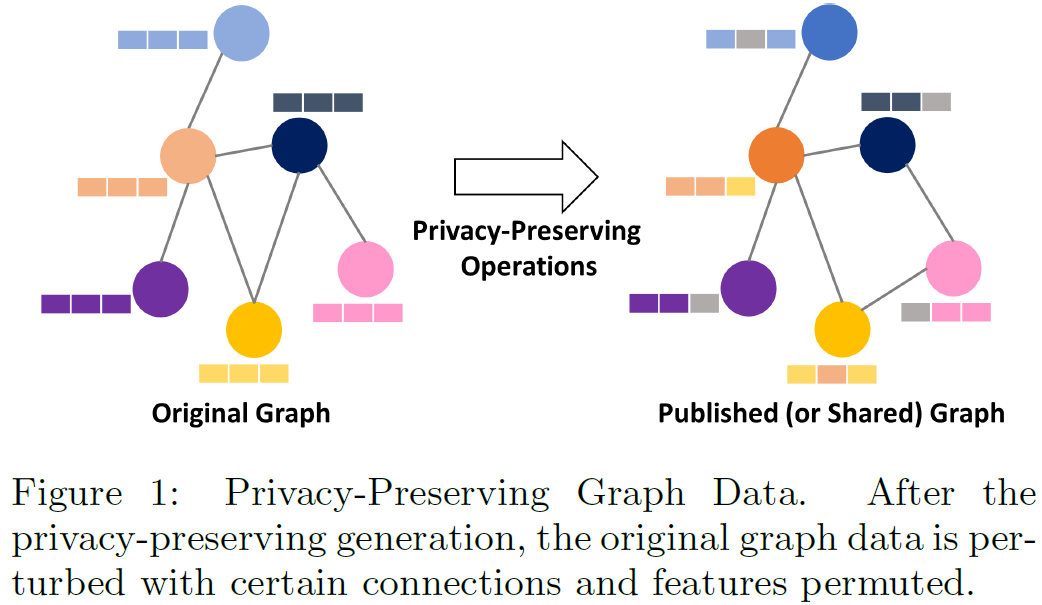
2. graph data privacy-preserving computation

   

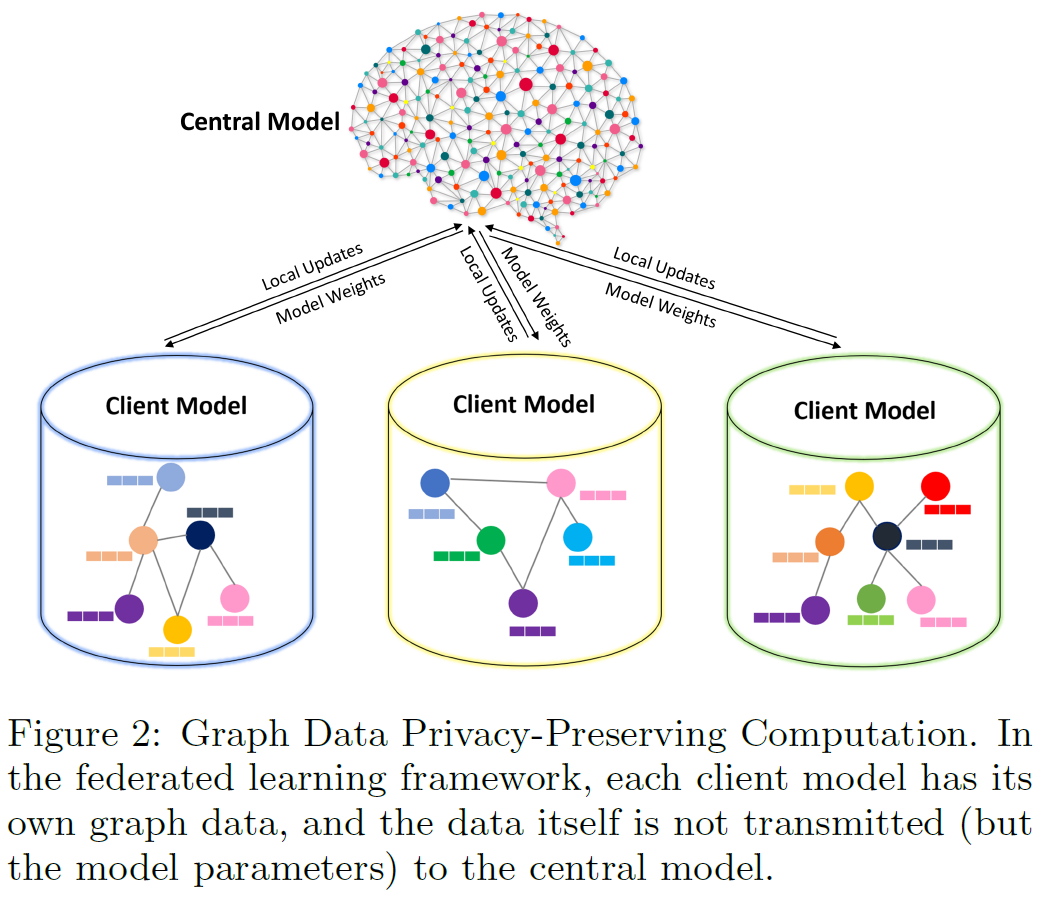
[2. Privacy-Preserving Graph Data]

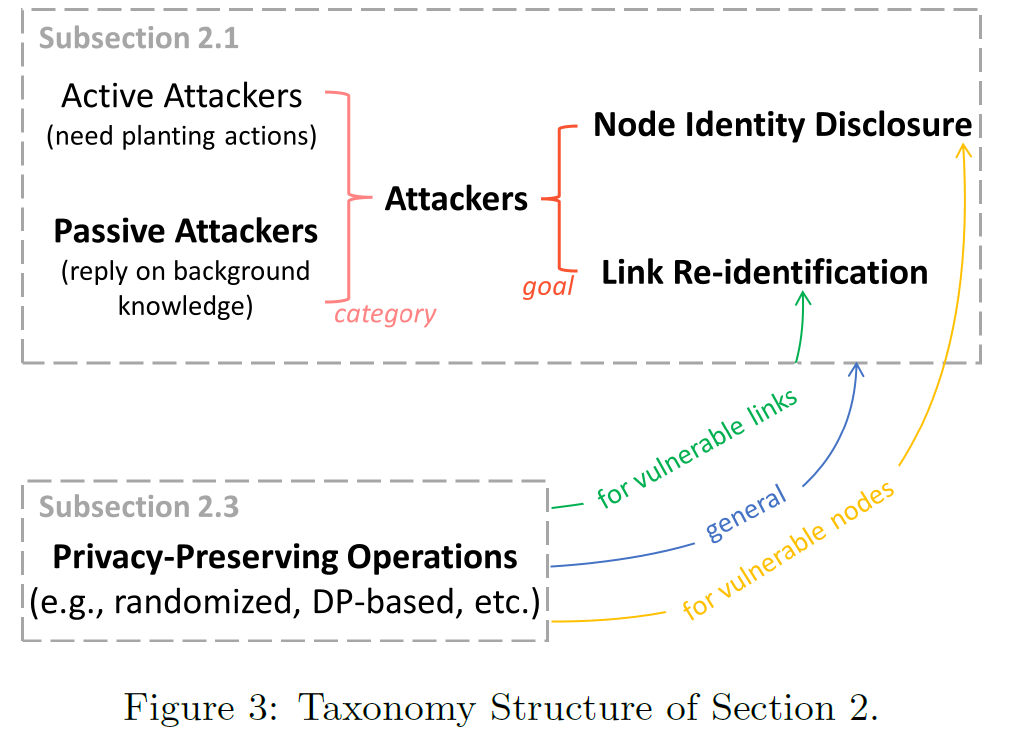
[2.1 Privacy Attackers on Graphs]

• aim of attackers: (1) whether edges exist (2) reveal true identities of targeted users

2.1.1. Category of Attackers

• active attackers
  • k 노드를 가지는 subgraph H를 만들어서 G에 넣은다음 s.t. $\abs{H\cap G}=b$, 나중에 G’로 published 됐을 때 G’ 안의 H를 찾고 b 개의 노드를 판명한다.
  • original graph에 published 되기 전에 접근함
• passive attackers
  • creation 대신 observation에 의존함
  • “node A는 degree가 2 이상”와 같은 external information 이용

2.1.2. Goal of Attackers

• diclosure of node identity: where is node A?
• link re-identification: determine private edges (not published) containing such as disease records
  • besides existence, we can infer weight or type of links

[2.2 Background Knowledge for Passive Attacks]

2.2.1 Background Knowledge for Node Identity Disclosure

• it helps them to detect “uniqueness” of victims
• target node의 background knowledge H를 알면, candidates를 줄일 수 있다
• method
  • vertex refinement queries
    • H0(x): node x의 label
    • H1(x): node x의 degree
    • Hi(x): multiset of Hi-1(x) queries on 1-hop neighbors of node x

    

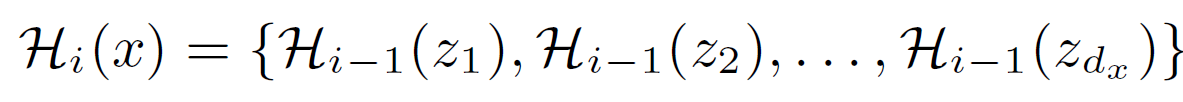
  • subgraph queries
    • existence of a subgraph
    • more general, flexible
    • note that different searching strategies can result in different subgraph structures
  • hub finger print queries
    • hub: node of a high degree and a high betweeness centrality
    • hub fingerprint: node’s connection to hubs
  • neighborhood relationship queries
    • rely on isomorphism of the ego-graph

2.2.2. Background Knowledge for Link Re-Identification]

• Method
  • link prediction probablistic model
    • 다른 종류의 background information이 probabilistic model을 만드는데 leverage 될 수 있다 (e.g node attributes, existing relationships, structural properties, inferred relationships)
      • mathematically, the existence of a sentsitive relation of node i and node j as: $P(e_{ij}^s;O)$ where $e^s_{ij}$: sensitive relationship, O: a set of observations

  • Randomization-based Posterior Probability

    

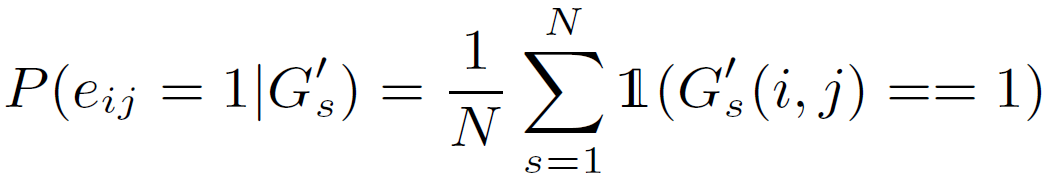
    • attacker applies randomization mechanism on G’ N times to get a sequence of G’s, and utilize that information

[2.3. Privacy-Preserving Mechanisms]

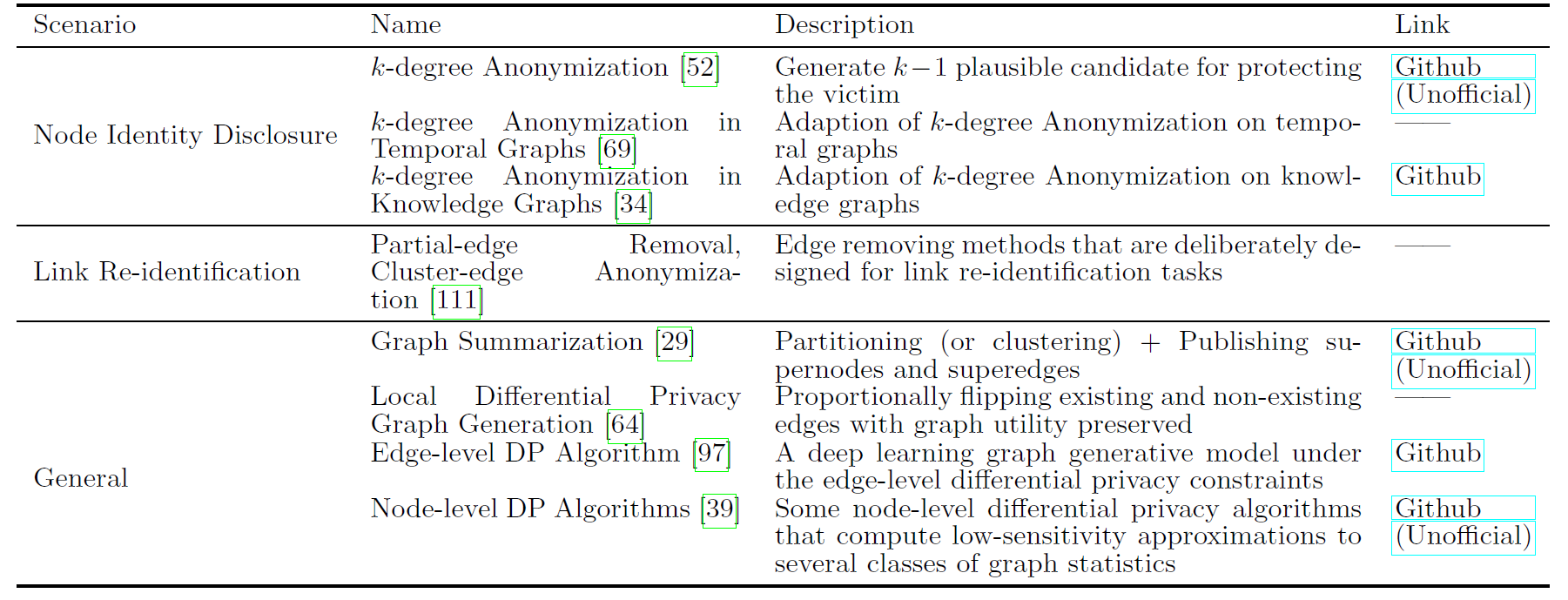
2.3.1. Protection Mechanism Designed for Node Identity Disclosure

• k-degree anonymization
  • target node x는 적어도 k-1의 node와 같은 degree를 share한다
  • degree distribution d → new distribution d’ (instanced by L1 distance)
  • construct G’ following d’

  Towards identity anonymization on graphs (KDD’08)

• k-degree anonymization in temporal graphs
  • ensure temporal degree sequence of each node is indistinguishable from that of at least k-1 other nodes
  • degree matrix D → D’
• k-degree anonymization in knowledge graphs
  • k-anonymity of the same attributes and degree
  • node feature와 degree에 따라 node를 clusters로 partition
• k-neighborhood anonymization
  • when an attacker knows background knowledge about neighborhood relationships
  • k-anonymity of neighborhood structure
  • use DFS search → vector → greedily make N(v) and N(u) same → construct G’
• k-automorphism anonymization
  • prevent from subgraph queries
  • G and G’ is k-automorphic
    • at least k-different matches in G’ for a subgraph query
  • KM algorithm

2.3.2 Protection Mechanism Designed for Link Re-Identification

• Intact Edges
  • remove all s type edges
• Partial-edge removal
  • remove part of sensitive edges
    • criteria: whether their existence contributes to the exposure of sensitive links
• Cluster-edge anonymization
  • partition G into clusters
  • remove edges inintra-clusters
  • preserve inter-cluster
  • can be interpreted as k-degree anonymization
• Cluster-edge anonymization with constraints
  • advanced version of above

2.3.3. General Privacy Protection Mechanisms

• Graph Summarization
• Switching-based Graph Generation
  • configuration model
  • preserve degree distribution
  • largely preserve original graph features (eigenvalues of adjacency matrix, Laplacian matrix)
• Spectral Add/Del and Spectral Switch
  • repeats adding and deleting edges
  • random switch
  • overall degree distribution not change
  • develop method that preserves largest aigenvalue of A and second smallest eigenvalue of L=D-A
• RandomWalk-Mod
  • copy each edge in G to G’ while guaranteeing the degree distribution of G’ is unchanged

Differential Privacy

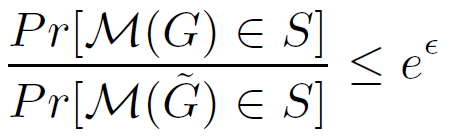
M: permutation

• It also categorizes to edge-level and node-level differential privacy

[2.4. Other Aspects of Graph Anonymization]

• 기존
  • 익명화 그래프 G’를 published 하는 대신, some non-trivial statistics를 랜덤화하고 이것을 relase하고 있음
  • 중요한 graph parameter를 보존하고 있음 (e.g. eigenvalue)

[2.5. Challenges and Future Opportunities]

2.5.1 preserving privacy for temporal graphs

• 기존 연구는 static graph를 주로 다루지만, 실생활 그래프는 거의 evolve함

2.5.2 preserving privacy for heterogeneous graphs

• 대부분 background knowledge는 structural queries를 사용
• node와 edge feature이 많은 경우, leaking sensitive information의 위험성을 증가시킴

⇒ 어떤 feature information이 heterogeneous와 time-eovolving graphs에서 중요할 것이고, 숨겨져야 하느냐

⇒ 이걸 위한 method는?

[3. Graph data Privacy-Preserving Computation]